Medición de la forma y el tamaño de la partícula utilizando análisis de imagen
Este documento describe de qué forma se calculan la forma y el tamaño de la partícula e ilustra cómo utilizar el análisis de la imagen para medir ambos.
El tamaño de la partícula:
Describir una partícula 3D suele ser un tema más complejo de lo que parece a simple vista. A los fines de practicidad u “operativos” es conveniente describir el tamaño de la partícula con un número único. Sin embargo, a menos que la partícula sea una esfera perfecta (algo poco común en las muestras del “mundo real”) hay muchas maneras de describir el tamaño de una partícula. Este es el desafío básico del análisis del tamaño de la partícula – ¿cómo describimos un objeto tridimensional con un número solo? El análisis de la imagen captura una imagen bidimensional de la partícula en 3D y calcula varios parámetros de forma y tamaño a partir de esta imagen bidimensional.
Uno de los diámetros de base calculados es el diámetro equivalente (diámetro CE por sus siglas en ingles) que es el diámetro de un círculo con la misma área que la imagen bidimensional de la partícula. Por supuesto las partículas de forma diferente tendrán una influencia en este diámetro equivalente pero, muy importante, es un número único que se agranda o achica junto con la partícula y es objetivo y repetible.
Diámetro CE
La imagen 3D de la partícula es capturada como una imagen bidimensional y convertida a un círculo de área equivalente a la imagen bidimensional. El diámetro de este círculo es luego informado como el diámetro equivalente de esa partícula (ver Figura 1). Por supuesto, un valor único de una partícula no es el tan buscado “número único para fines operativos”.
Es improbable que tenga relevancia estadística ya que el valor único depende de la partícula individual seleccionada. Debe medirse un número de partículas representativo de su muestra como un total y deben generarse parámetros estadísticos. Un número de caracterización único más apropiado sería el promedio de todos los diámetros equivalente CE por ejemplo. Una vez generada una distribución, pueden calcularse con facilidad todos los parámetros estadísticos como promedio, medio, modo, desviación típica, D 10, percentiles D 90 etc. Muchas muestras del “mundo real” tienen forma amplia como la distribución “normal” o “gaussiana”. Esto nos permite aplicar métodos estadísticos para evaluar los parámetros de confianza y hacer recomendaciones con respecto al número mínimo de partículas a analizar para alcanzar un nivel razonable de significación estadística.
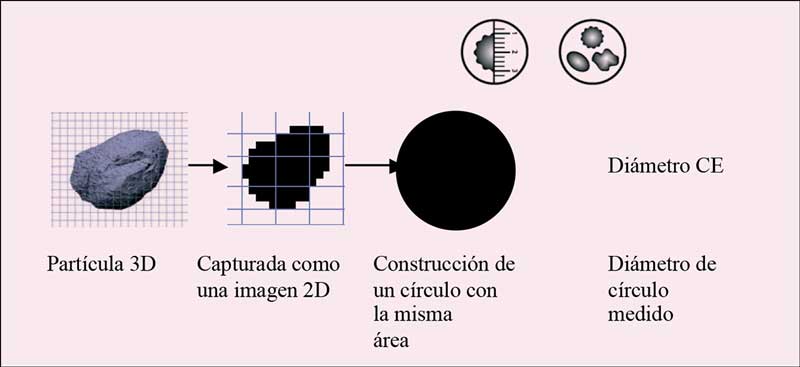
Figura 1: Calculo del diámetro equivalente CE.
¿Qué es la forma de la partícula y por qué es importante?
Si describir un tamaño de partícula 3D es complejo, entonces ¡cuantificar la forma es todavía más complicado! Hay un número casi infinito de maneras de describir una forma compleja y al hacerlo parecemos desviarnos de nuestro objetivo de reducir una muestra a un número cuantificable. Entonces, ¿por qué medir la forma? Medir el tamaño solo a veces no es lo suficientemente sensible para identificar diferencias sutiles pero importantes entre las muestras. Algunos grupos de muestras pueden ser diferentes por una cantidad tan pequeña que esta diferencia se pierde durante la traducción a un diámetro equivalente a una esfera o equivalente a un círculo. Por ejemplo, considere las 3 formas a continuación. Estas tres formas tienen la misma área = 4 unidades cuadradas. Cuando se las convierte a un diámetro equivalente al círculo dan el mismo resultado – un diámetro equivalente al círculo de 2.257 unidades.
Esto resalta la desventaja principal de medir el tamaño solamente – muestras de formas muy diferentes podrían ser caracterizadas como idénticas simplemente porque tienen áreas bidimensionales proyectadas similares. Con frecuencia, la forma de la partícula tiene una importante influencia sobre los parámetros de desempeño del producto final como la fluidez, la eficiencia abrasiva, la biodisponibilidad, etc. por eso es necesario contar con alguna manera de caracterizar la forma.

Morfologi G3: Sistema óptico totalmente automatizado para caracterización detallada de partículas, utilizando las técnicas de imágen y el análisis datos, con la mínima intervención del usuario.
Tres factores de forma comúnmente utilizados – circularidad, convexidad y elongación
Una medición de la forma consiste en cuantificar la “cercanía” a un círculo perfecto. Para esto, usamos el parámetro de circularidad que se define del siguiente modo:
Circularidad = 4πA/ P2
Donde A es el área de partícula y P es el perímetro.
La circularidad es una relación del perímetro de un círculo con la misma área que la partícula dividida por el perímetro de la imagen de la partícula. Hay definiciones alternativas de Circularidad pero la definición antes mencionada tiene un término al cuadrado en el numerador y denominador para sensibilizar el parámetro a las variaciones más sutiles en la relación área-perímetro.
Por esto nos referimos a este parámetro con mayor precisión como la Circularidad HS (para la Sensibilidad Elevada). La circularidad tiene valores en el rango 0-1. Un círculo perfecto tiene una circularidad de 1 mientras que un objeto irregular o muy “puntiagudo” tiene un valor de circularidad más cercano a 0. La circularidad es la sensibilidad a la forma general y la aspereza de la superficie. Analice las siguientes formas – observe como la circularidad está afectada por la forma general y la simetría, y la aspereza de la superficie. La circularidad es una buena medición de lo que en términos humanos, podríamos describir como la “desviación de un círculo perfecto”: Ver Figura 4
Sin embargo, es importante recordar que es improbable que un descriptor de forma único discrimine perfectamente y caracterice todas las aplicaciones y las diferentes combinaciones de formas. Observe que la forma larga de elipse (Figura 3, parte superior derecha) tiene exactamente la misma circularidad que la forma compacta y puntiaguda (Figura 3, parte inferior izquierda). Por lo tanto, se desarrollaron una variedad de parámetros de forma para ser utilizados como un “kit de herramientas” – las aplicaciones diferentes requieren de herramientas diferentes. Por ejemplo, una aplicación relacionada con partículas perfectamente esféricas y que mida, tal vez a los fines de Control de calidad, la desviación con respecto a la esfera perfecta utilizaría la circularidad como el parámetro discriminatorio.

Figura 2 – 3: Formas muy diferentes con diámetro CE idéntico.
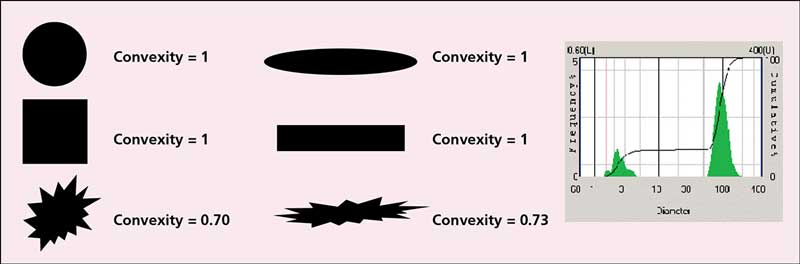
Figura 4: Ilustración de descriptor de forma de convexidad forma descriptor.
Sin embargo, la circularidad no sería apropiada para una aplicación con partículas “puntiagudas” y elípticas presentes.
Otros dos parámetros de forma comúnmente utilizados son la convexidad y la elongación.
Convexidad
La convexidad es una medición de la aspereza de la superficie de una partícula y se calcula dividiendo el “perímetro de casco convexo” por el perímetro de la artícula. La forma más sencilla de visualizar el “perímetro de casco convexo” es imaginar una banda elástica ubicada alrededor de la partícula. La convexidad también tiene valores que van de 0 a 1. Una forma homogénea tiene una convexidad de 1 ya que el perímetro de casco convexo es exactamente el mismo que el perímetro real. Un objeto irregular o muy “puntiagudo” tiene una convexidad más cercana a 0 ya que el perímetro real es más grande que el perímetro de casco convexo debido a las características de la superficie fina.
Analice las formas en la Figura 4 – observe cómo la convexidad no está afectada por la forma general. Una smooth needle tiene la misma convexidad que un smooth circle.
Elongación
La elongación se define como [1-relación de aspecto] o [1- ancho/longitud]. Como el nombre lo indica, es una medición de la elongación y nuevamente tiene valores en el rango 0 a 1. Una forma simétrica en todos los ejes como un círculo o un cuadrado tendrá un valor de elongación de 0 mientras que las formas con relaciones de aspecto grande tendrán una elongación más cercana a 1. Analice las formas en la Figura 5 –observe como la elongación no resulta afectada por la aspereza de la superficie– un elipse regular tiene una elongación similar a una elipse puntiaguda de relación de aspecto similar. Junto con la sensibilidad obtenida a partir de la capacidad para medir la forma, el análisis de imagen proporciona otros dos beneficios importantes: la resolución basada en número y la grabación de imágenes. Ambos le brindan al usuario información adicional que contribuye a una comprensión más profunda del producto o proceso de fabricación.
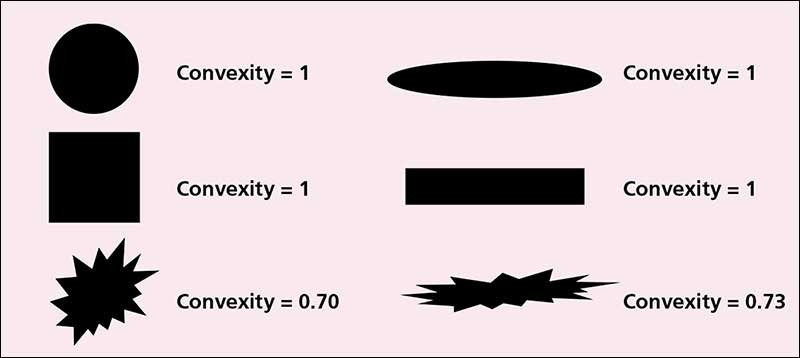
Figura 5: Ilustración de descriptor de forma de convexidad forma descriptor.
¿Qué significa resolución “basada en número”?
Algunas aplicaciones, particularmente aquellas donde la detección de números pequeños de partículas relativamente pequeñas (finas) o la detección de partículas externas son importantes, requieren de la resolución de un sistema basado en número. No todas las aplicaciones necesitan de esta sensibilidad basada en número; por lo general tiene sentido beneficiarse de la velocidad y conveniencia de los métodos de conjunto.
Los métodos de conjunto para la determinación del tamaño de partícula por lo general proporcionan información sobre lo que se conoce “como “base – volumen”. Esto significa que la contribución que cada partícula realiza es proporcional a su volumen – las partículas grandes dominan la distribución y la sensibilidad a las partículas pequeñas se reduce ya que su volumen es mucho más pequeño que el de las más grandes.
El análisis de la imagen brinda información sobre lo que se conoce como “base-número”: Esto significa que la contribución que cada partícula hace a la distribución es la misma: una partícula muy pequeña tiene exactamente la misma ponderación que una partícula muy grande. A los fines de diagnostico o identificación y resolución de problemas, la presencia de finos podría ser muy importante para comprender por completo el proceso de fabricación y es posible que se requiera sensibilidad extra para los fines de análisis de imagen.
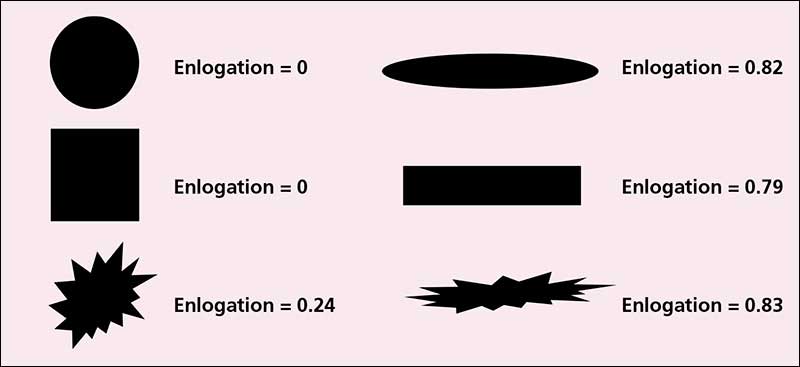
Figura 6: Ilustración de descriptor de la forma de elongación.
Grabación de Imágenes
La capacidad de visualizar imágenes de partículas individuales le dan al usuario un nivel extra de verificación que respalda los datos cuantitativos y ayudan a optimizar el desarrollo del método y la preparación de la muestra.
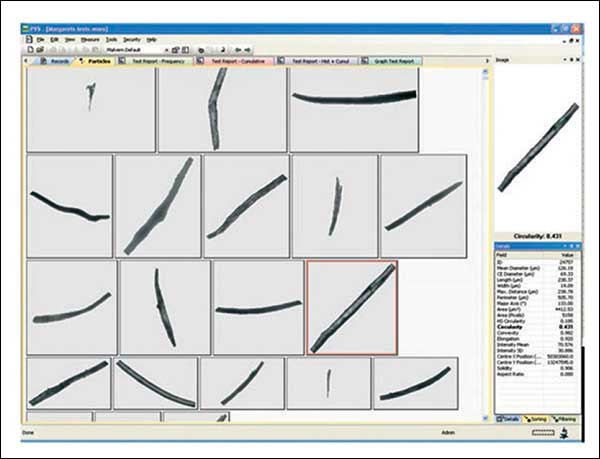
Esta capacidad es particularmente útil para determinar si una partícula de forma irregular es una partícula primaria genuina o un aglomerado de partículas más pequeñas por ejemplo. Se pueden entonces ordenar, filtrar y clasificar las imágenes de todas las partículas según los requerimientos del usuario. La Figura 7 muestra una clara aglomeración de las partículas principalmente esféricas. Pueden ser identificadas visualmente a partir de las imágenes y son también cuantificables con el uso de un parámetro de forma como la circularidad. Todos los aglomerados tendrán un valor de circularidad más bajo que las partículas esféricas primarias, por lo tanto clasificar y filtrar sobre la base de la circularidad identificará rápidamente el nivel de aglomeración en una muestra.
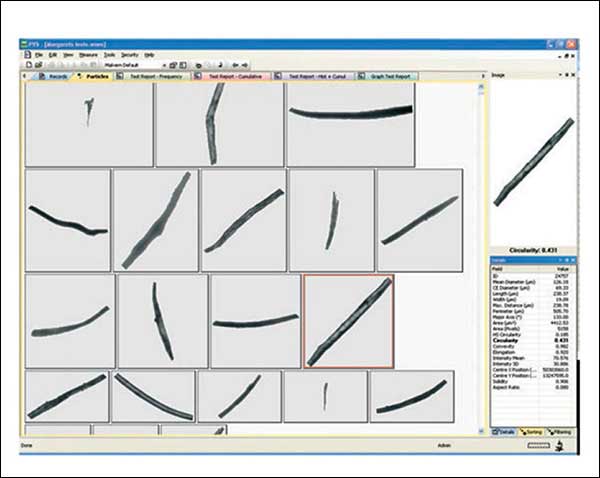
Figura 7: Visor de imagen de partícula mostrando aglomerados.
La Figura 8 muestra partículas con una forma clara de aguja. Pueden detectarse visualmente con las imágenes reales y también estadísticamente usando un parámetro de forma como la elongación.